[AI] Neural Network, 활성 함수, MLP

Neural Network (신경망)

인공신경망 뉴런 모델은 생물학적인 뉴런을 수학적으로 모델링한 것입니다.

여러개의 뉴런으로부터 입력 값을 받아서 세포체(cell body)에 저장하다가 자신의 용량을 넘어서면 외부로 출력 값을 내보내는 것처럼, 인공신경망 뉴런은 여러 입력값을 받아서 일정 수준을 넘어서면 활성화되어 출력값을 내보냅니다.

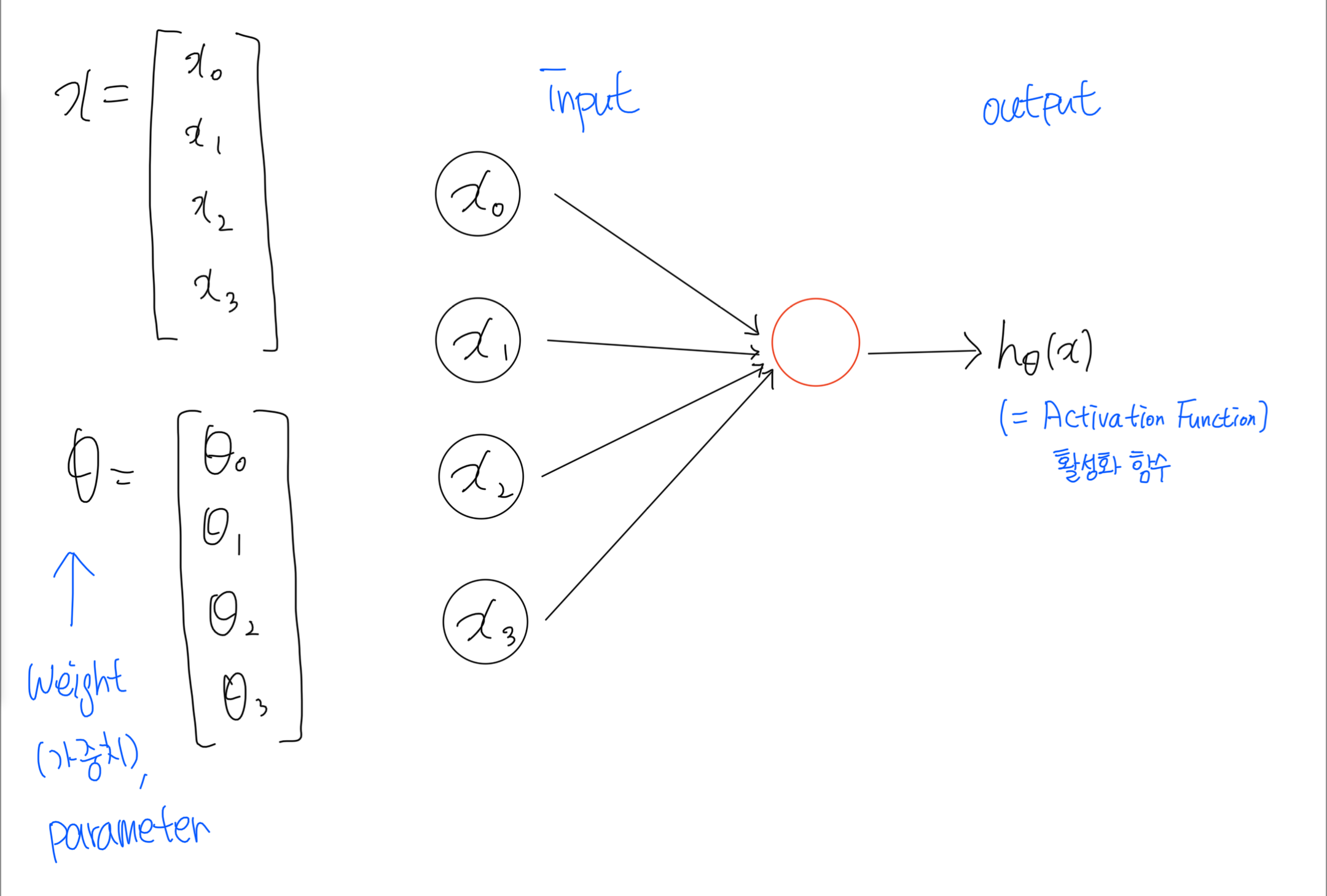
신경망은 선형 모델과 활성함수를 합성한 함수입니다.

활성화 함수

활성화 함수는 선형 함수가 아닌 비선형 함수여야 합니다.

선형 함수란 출력이 입력의 상수배만큼 변하는 함수입니다.

예를 들어 f(x) = wx + b 일 때, (w, b는 상수) 직선 그래프가 나옵니다.

반대로 비선형 함수는 직선 1개로 그릴 수 없는 함수입니다.

인공 신경망의 능력을 높이기 위해서는 은닉층을 계속 추가해야 합니다. 그런데 만약 활성화 함수로 선형 함수를 사용하게 되면 은닉층을 쌓을 수가 없습니다.

예를 들어, 활성화 함수는 f(x) = wx일 때, 은닉층 2개 추가하면 출력층을 포함하여 y(x) - f(f(f(x)))가 됩니다.

이는 w*w*w*x 입니다. 즉, w의 세제곱을 k라고 정의하면 y(x) = kx로 표현이 가능합니다.

이는 선형 함수로 은닉층을 여러번 추가하더라도 1회 추가한 것과 차이가 없음을 나타냅니다.

활성함수를 쓰지 않으면 딥러닝은 선형모델과 차이가 없습니다.

많은 활성화 함수가 있지만, 대표적으로 Sigmoid, Tanh, ReLU 함수가 있습니다. 딥러닝에서는 현재 ReLU함수를 많이 사용하고 있습니다.

Sigmoid function

$$
\sigma(x) =\frac{1}{1+e^{-x}}
$$
sigmoid function은 활성화 함수로 많이 사용되며, 모든 실수 값을 0과 1사이 값으로 변환시킵니다.

일정 값을 넘어서면 1, 그 이하는 0 값을 출력합니다.

입력 값 x와 각각의 입력 값에 대한 가중치(weight)로 계산된 결과를 sigmoid함수에 입력하여 0과 1사이 값으로 바꿉니다.

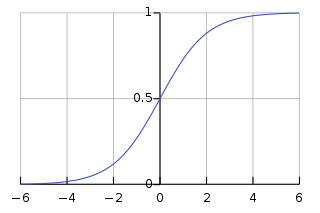
출처 : https://en.wikipedia.org/wiki/Sigmoid_function

sigmoid function 문제점

미분을 해서 기울기(gradient)를 구할 때 발생합니다.

sigmoid 함수의 그래프를 보면 출력 값이 0또는 1에 가까워지면 그래프의 기울기가 완만해지는 것을 볼 수 있습니다.

기울기가 완만한 구간은 미분 값이 0에 가까운 아주 작은 값이고, 기울기가 가파른 구간의 최대 미분 값은 0.25입니다.

즉, 시그모이드 함수를 미분한 값은 적어도 0.25이하입니다.

sigmoid함수를 활성화 함수로 사용하여 인공 신경망의 층을 쌓는다면, 가중치와 편향을 업데이트 하는 과정인 역전파 과정에서 0에 가까운 값이 누적해서 곱해지게 되어 앞단의 기울기(미분 값)이 제대로 전달되지 않게 됩니다. 이러한 현상을 _기울기 소실(Vanishing Gradient)_문제 라고 합니다.

시그모이드 함수를 사용하는 은닉층의 개수가 많아 질 수록 0에 가까운 기울기가 계속 곱해지면, 앞단에서는 기울기를 거의 전파받을 수 없게 됩니다. 즉, 매개변수 w가 업데이트 되지 않아 학습이 되지 않습니다.

결론적으로 시그모이드 함수의 은닉층에서의 사용은 지양됩니다. 주로 이진 분류를 위해 출력층에서 사용합니다.

Hyperbolic tangent function

입력 값을 -1과 1사이의 값으로 변환합니다.

sigmoid와 같은 문제가 발생합니다. 그러나 tanh함수는 sigmoid함수와 다르게 0을 중심으로 하고 있어 최대 미분 값은 1로, sigmoid함수의 최대 미분 값인 0.25보다는 큽니다. 즉, sigmoid함수보다는 미분 값이 크게 나옵니다. sigmoid함수보다 기울기 소실 증상이 적은 편입니다.

ReLU

인공 신공망의 은닉층에서 가장 인기있는 함수입니다.
$$
f(x) = max(0,x)
$$

ReLU함수는 음수는 0, 양수는 그대로 출력하는 특징인 함수로, 출력값이 특정 양수값에 수렴하지 않습니다. 0 이상의 값의 경우 미분 값이 항상 1입니다. 깊은 신경망의 은닉층에서 sigmoid함수보다 훨씬 잘 작동합니다. 또한 sigoid, tanh함수와 같이 어떤 연산이 필요한 것이아니라 단순 임계값이므로 연산 속도도 빠릅니다.

하지만 ReLU에도 문제점이 있습니다. 입력값이 음수면 기울기(미분값)도 0입니다. 그리고 이 뉴런은 다시 회생하는 것이 매우 어렵습니다. 이 문제를 _dying ReLU_라고 합니다.

Softmax function

은닉층에서 ReLU함수들을 사용하는 것이 일반적입니다. 반면, softmax함수는 sigmoid함수처럼 출력층에서 주료 사용됩니다. sigmoid함수가 이진 분류(binary classification) 문제에 사용된다면, softmax함수는 3가지 이상의(상호 배타적인) 선택지 중 하나를 고르는 다중 분류(MultiClass Classicifation)문제에 주로 사용됩니다.

딥러닝으로 이진 분류를 할 때는 출력층에 Logistic Regression(로지스틱 회귀)를 사용하고, 다중 클래스 분류 문제를 풀 때에는 출력층에 Softmax Regression을 사용합니다.

Multi-Layer Perceptron

단층 perceptron 형태에서 은닉층이 1개 이상 추가된 신경망을 다층 퍼셉트론(MLP)라고 합니다.

MLP는 Feed Forward Neural Network(FFNN)의 가장 기본적인 형태입니다. 피드 포워드 신경망은 입력층에서 출력층으로 오직 한 방향으로만 연산 방향이 정해져 있는 신경망을 말합니다.

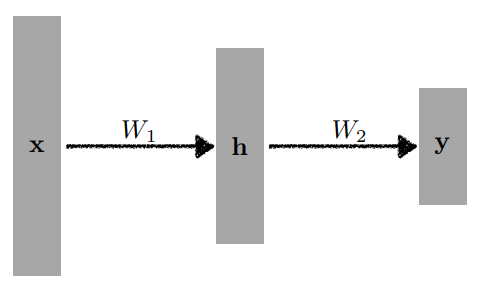
$$
y = W_2^{T}h = W_2^{T}p(W_1^{T}x)
$$

 

Layer는 더 깊이 쌓을 수 있습니다.

 

loss function

$$y_i^{(d)} : 실제 값$$

$$\hat{y}_i^{(d)} : 예측 값$$

▶ Regression Task (회기 문제)

Mean Squared Error(MSE) 평균 제곱 오차
$$
{MSE=\frac 1 N}\sum_{i=1}^{N}\sum_{d=1}^{D}(y_i^{(d)}-\hat{y}_i^{(d)})^{2}
$$

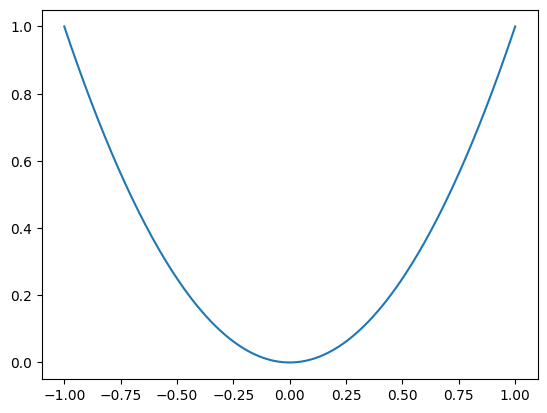
y = x^2

평균 제곱 오차는 가장 많이 쓰이는 손실 함수 중 하나이며, 예측 값과 실제 값 사이의 평균을 제곱하여 평균을 계산한 값입니다. 차이가 커질수록 제곱 연산으로 인해 값이 뚜렷해지며 제곱으로 오차가 양수, 음수 상관하지 않고 값을 증가시킵니다. MSE는 실제 정답에 대한 정답률의 오차뿐만 아니라 다른 오답들에 대한 정답률 오차 또한 포함하여 계산한다는 것이 특징입니다. 최적 값에 가까워질 경우 이동거리가 다르게 변화하기 때문에 최적 값에 수렴하기 용이합니다. MSE의 단점으로는 값을 제곱하기 때문에 1미만의 값은 더 작아지고, 그 이상의 값은 더 커지는 왜곡이 있을 수 있습니다.

 

▶ Classification Task (분류 문제)

Cross Entropy(CE)

(= binary entropy, log loss)

$$
{CE=\frac 1 N}\sum_{i=1}^{N}\sum_{d=1}^{D}(y_i)^{(d)}log\hat{y}_i^{(d)}
$$

Entropy 는 불확실성으로, Entropy가 높다는 것은 정보가 많고 확률이 낮다는 것을 의미합니다.

분류 문제에서 데이터의 라벨은 one-hot encoding을 통해표현됩니다. one-hot encodeing은 class의 종류가 N개 이고, 특정 데이터가 i번째 클래스에 속할 때, i 번 째 원소만 1, 나머지는 0으로 채운 N차원 vector로 바꿔주는 것입니다.

입력 데이터의 특성(feature)값이 모델을 통과하면 출력 레이어의 softmax함수에 의해 각각 class에 속할 확률이 계산됩니다. 이 확률 값들이 모델이 추정한 확률 분포를 구성하는 값들입니다.

 

▶ Probabilistic Task (확률 문제)

 

Likelihood (가능도, 우도 함수)

데이터가 특정 분포로부터 만들어졌을 확률.(파라미터의 분포 P(theta)가 정해졌을 때, x라는 데이터가 관찰될 확률)

주어진 파라미터 분포에 대해서 우리가 가지고 있는 데이터가 얼마나 '그럴듯한지' 계산한 값입니다.
$$
L(\theta) = p(X|\theta) = \prod_{n=1}^{N}{p(X_n|\theta)}
$$

 

Maximum Likelihood Estimation(MLE) 최대 가능성 추정

가능도 중에 높은 가능도가 있을 것이고, 이는 제공한 데이터 샘플에 가장 잘 맞는 모델이나 분포의 파라미터 theta가 존재한다는 뜻입니다. 따라서 최적의 파라미터 theta를 찾는다는 개념입니다.
$$
{MLE=\frac 1 N}\sum_{i=1}^{N}\sum_{d=1}^{D} logN(y_i^{(d)};\hat{y}_i^{(d)},1) (=MSE)
$$

데이터들의 likelihood값을 최대화하는 방향으로 모델을 학습시키는 방법입니다.

 

 

 

참고

https://wikidocs.net/24987